Visualizing Twitter Data

Inspired from this post on plotting the frequency of Twitter hashtags over time, I was interested in trying to apply this to soccer some way. While not the most technical analysis, I thought it would be interesting to use this tool to analyze transfer rumors.

To summarize the process quickly, there is a package in R (open source statistical software) called TwitteR which allows you to pull Twitter data. It's actually a fairly easy process, especially if you follow the tutorial in the link at the beginning of this post.

As most Twitter users know there is a seemingly unlimited number of transfer rumors circulating Twitter. These range from being fairly plausible to pretty ridiculous ("Ronaldo to the Philadelphia Union???).  As a Manchester City supporter, I was curious at looking at a few popular transfer rumors related to City.

Robin van Persie to Manchester City:

Yes, this is definitely a rumor, and yes, it is probably not going to happen. But I was still curious. Below is a plot of the frequency of the number of tweets that include "Robin van Persie" and "Manchester City". Of course, this is an imperfect method, but it still gives us an idea of what is going on in the Twitter transfer rumor world.

To explain, the graph below measures the number of tweets described above at a 2 hour interval for the past week. This means the height of every line gives us the number of tweets referencing RVP and City in that 2 hour interval.

Carlos Tevez to AC Milan:

After Tevez's past season with the club, there are obviously transfer rumors concerning Tevez all over the place. Because of this, it was hard not to want to look at the data on Tevez. I picked AC Milan because it seemed like the club he had the highest likelihood of going to. Like above, I searched for tweets that included "Carlos Tevez" and "AC Milan". The frequency of these tweets, in 2 hour intervals, is plotted below.

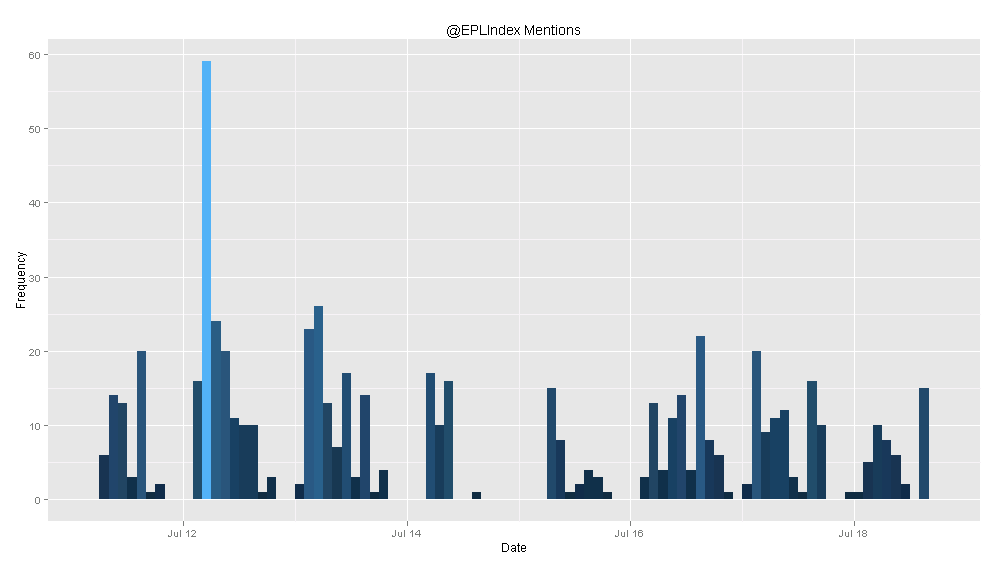
You can try to analyze these graphs to find some meaning, but they are more just a fun exercise than anything else. The TwitteR package lets you do other cool things, like plot the frequency of Twitter mentions for a user. I did this for another site I write for, EPL Index. They tend to get a lot more mentions than @SoccerStatistic does, so I thought it would be more interesting to plot the frequency of @EPLIndex mentions. Again, the intervals are every 2 hours.

Like I said before, this analysis is not very insightful or ground-breaking, but still pretty cool nonetheless. The possibilities for future analysis like this are almost endless, so if people have good ideas of Twitter data to visualize, I'd love to hear them.

Answer to my Question via Twitter Posted Earlier

The question I asked earlier today via my twitter @SoccerStatistic was, "Which statistic correlates best with a team's point total?" The options were goals against, corners, goals for, and shots on target. The answer is extremely surprising to say the least.

Another way to ask the question is "Given the goals against, corner, goals for, or shots on targets total for a team in the EPL, which variable would allow you to best predict the point total of the team?" Turns out the answer is not goals for, goals against, or even shots on target. Yep, its the corner total. This means the amount of corners a team accumulates during the season is a better indicator of the team's standing than the other variables. To me, this is mind-boggling. The point of the game is to score more goals than your opponent, yet the amount of corners predict point totals the best.

The way to figure this out is with linear regressions between points and the 4 statistics in questions using season totals for EPL teams. A linear regression tells us how strong the linear relationship between two variables are with a number called the correlation coefficient. A value of 0 would mean there is absolutely no relationship, and a value of 1 would mean a perfect linear relationship. Below is a chart of the 4 variables and their correlation coefficient value. The absolute value of the correlation coefficients are given below, as goals against obviously has a negative relationship with.

Corners just edge out goals for and goals against as the strongest relationship. There is only really one explanation I can think of to explain this: Corners result from pressure on the goal, and more corners would mean more pressure on the goal which corresponds with more wins and a higher point total. Still, the fact that the relationship is stronger than the relationships between points and goals for and points and goals against really amazes me.

A few things to point out: First, the best way to really predict a team's success is with their goal differentials. However, it is still interesting that corners have the strongest relationship of the 4 variables above. Second, the relationship between corners and points shouldn't be read in to too much. This doesn't mean that if a team goes out trying to get more corners they will be more likely to win the game; instead it means that better teams tend to earn more corners based on the way they are playing.

This also leads in to something else I will be working on in the near future which relates somewhat. Are the amount of goals scored by a player a good indication of the quality of the player? Forwards are the highest paid players in soccer, but what if goal scorers are significantly overvalued? Is it right when we say "Player x is a better player than player y because he scored more goals this season"? I think there are a number of ways to test these questions, so check back in the coming week for some results and analysis.