Problems with an Adjusted Plus Minus Metric in Football

Michael Essien

What would be the perfect, all-encompassing football statistic? Something that takes in to account both offensive and defensive skill. Something that measures what value a player adds to his club. All in all, a statistic that quantifies the individual impact a player has on improving (or worsening) his club's ability to score goals and limit (or not) goals against.

Some people have made attempts at this in the past. One example are OptaJoe's tweets (@OptaJoe) about club's winning percentages with and without a player. Here is one example: "10 - Since January 2005, Everton have averaged 61 points per season with Arteta playing, compared to 51 points without him. Lynchpin." These statements are simple, easy to understand, and at first glance seem to be informative. On his blog 5 Added Minutes, Omar Chaudhuri has correctly pointed out that these statements tend to be entirely misleading. As Omar shows, the problem is that these statements are not controlling for the strength of the opponent, the venue of the game, or really anything else, in these games.

My idea was to create a metric that would control for all of these factors to truly understand every player's worth to their club. Being a big ice hockey fan (specifically the Boston Bruins, if you are wondering) I thought that the plus minus statistic might be able to be applied to football. For those of you not familiar with this statistic, plus minus basically measures a club's net goals when that player is on the ice/field. When the team scores a goal when the player is playing, the player's plus minus increases by one. Conversely, when their team concedes a goal when they are playing, their plus minus decreases by one. The idea is that, over the season, the best players will have the highest plus minus.

I faced the same problem as before though, as this does not control for the strength of the opponent, the strength of the team the player is playing with, and where the game is being played. For example, a poor player on a top club would naturally have a higher plus minus than a good player on a poor club.

To fix this, I applied an analysis used in basketball to create an adjusted plus minus statistic. This was created by Dan Rosenbaum, and if you are interested the explanation can be found here

Without going in to too many technical details, the adjusted plus minus metric is created using a massive regression. The right hand side variables are variables for every player, while the left hand side are goals for. Each observation is a unit of time during a game where no substitutions are made. Each player variable is a 1 if the player is playing at home during that unit of time, a -1 if they are playing away, and a 0 if they are not playing. The significance behind this methodology is that it controls for each player's team, venue, and opponents. If you want to know more about the methodology, read the link above. The data is from the 2010/2011 season and is provided by Infostrada Sports  (@InfostradaLive on Twitter).

The main problem with this as some, including Albert Larcada (@adlarcada_ESPN), pointed out on Twitter, is that there is multicollinearity in the regression. This arises because, unlike in basketball, there are not many scoring events. What happens is that many players are highly correlated in the model. This throws off the adjusted plus minus values for each player, so we should not take anything from the results.

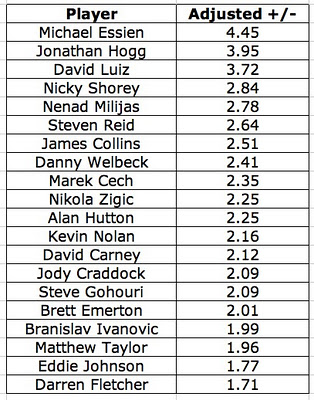
With that in mind, here are the results that I came up with. Again, these results are likely not correct, but I thought people might be curious to see them anyways:

Because I (a) spent a lot of time on this and (b) think it is important post work even if it doesn't necessarily work out, I went ahead and wrote this post. Keep in mind that the results above don't really mean much. The values are also not statistically different from 0. In other words, the standard errors on all the values are large enough so that we cannot say that they are statistically different from 0. This is another reason why the results are not very reliable. However, I think that the adjusted plus minus statistic could be the first step to creating metrics that truly capture the actual value of a player. Most statistics used (assists, goals, etc.) can be thrown off because they are highly dependent on the team the player plays for.

One way to fix the problem of mulitcollinearity is to use a different statistic that occurs more often, and is highly correlated with goals. I think the best option for this would be shots on goal. This way, you could create a statistic that controls for the player's team, opponents, and venue, and measure how many net shots on goal occur when they are on the field. Just a thought on a possibility of something to look at in the future.

The data used for this is provided by

Infostrada Sports

 (@InfostradaLive on Twitter). Special thanks to Simon Gleave (@SimonGleave on Twitter) for helping me with the data.

How to Succeed in the EPL: Chances Created and Chance Conversion

A common statistic that many people have begun to value and notice a lot recently is the chances created statistic. Chances created, according to Opta's website, is defined as "assists plus Key passes" where a Key Pass is "the final pass or pass-cum-shot leading to the recipient of the ball having an attempt at goal without scoring" (Opta is a company that tracks and generates a ton of data in soccer). So basically, any pass that leads to a shot is considered a chance created.

Swansea's Mark Gower is a perfect example of a player highlighted by the chances created statistic.

Chances Created

The appeal of this measure is that it can value players that play on weaker teams better than assists do. For a player on a weaker team, it is harder to record assists since they are playing with teammates that are less likely to score. Chances created is a fairer statistic because it does not value the strength of your teammates as much. Overall, it can highlight creative players that are often overlooked because they are on weaker teams and do not have as many assists.

Do Chances Created Actually Matter?

With all this in mind, I was curious to find the actual worth of the chances created statistic. One way to measure this is to look at how chances created and wins are correlated. To make it a little easier, I looked at the relationship between goals scored and chances created for EPL teams. In other words, do teams that have more chances created score more? Do teams with less chances created score less? The answer, in short, is yes, they are correlated. Below is a scatterplot of the relationship. There is a clear positive relationship between chances created and goals in the EPL last season. The coefficient is statistically different than 0 (p=.000), which tells us that there is extremely strong evidence that there is a positive relationship.

Chance Conversion Percentages

This is only half the story though. Some teams get a lot of shots off, but either because they are not good at shooting or are taking shots that have a smaller chance of going in, some of these teams have a low number of goals because they have a poor conversion percentage for shots. The conversion percentage is defined as the goals divided by the total number of shots (excluding blocked shots). Below is a scatterplot similar to the one above, this time with conversion percentages on the x-axis. The conversion rates are rounded to 2 decimal places, hence the bunching. Again, this shows a positive relationship between conversion percentage and goals. Teams with higher conversion rates tend to score more and vice versa. This relationship is also statistically different from 0 (p=.002). A quick note: the product of chances created and conversion rate is very close to the number of goals a club has scored. I'm pretty sure the discrepancy comes from including blocked shots in shots attempted, but not in conversion rates.

EPL 2010-2011, Chances Created and Conversion %

With this in mind, I created a scatterplot of conversion rates and chances created for EPL teams last season. The plot shows that clubs found scoring success in different ways. The Manchester clubs did it by being efficient scorers; they had conversion percentages of .15 and .16. Chelsea and Tottenham were on the other end of the spectrum with higher chances created, but lower conversion percentages (.12 for both). The graphic also shows that West Ham did not struggle because they were not creating chances; they struggled because they had a low conversion percentage (.10). On the other hand, Birmingham struggled because they failed to create enough chances to score, despite a decent conversion percentage of .12.

EPL 2011-2012 thus far, Chances Created and Conversion %

What about this year? Below, I created the same scatterplot as above, this time for the current season. City's dominance is really highlighted. They are leading in both chances created AND conversion percentage, hence the massive number of goals this year. Again, United seems to be scoring because of their high conversion percentage. QPR and United actually have very similar number of chances created, United just finishes their chances with a much higher percentage. Liverpool sticks out because of their high number of chances created, but really low conversion percentage (.09).

Conclusion

The bottom line is that creating chances and conversion rates are the key to understanding goal scoring. A club can succeed with a high conversion rate (United) or by creating a lot of chances (Liverpool). A club can really dominate by doing both well (City). The graphic above can also suggest what kind of players each club needs. For example, Manchester United and Newcastle would benefit by picking up a creative midfielder who creates more chances, and Liverpool and QPR would benefit by picking up a more efficient scorer. The scatterplot also tells us why some clubs struggle. Wigan needs to up their conversion percentage (currently a dismal .06) and Stoke needs to create more chances. City, on the other hand, should just continue to buy all the best players.

All data comes from eplindex.com (@EPLIndex)

An Analysis of the Performance of Promoted Clubs

Joey Barton, of newly promoted QPR

An aspect of English football that I love that does not exist in American sports is the promotion/relegation aspect. It makes not just the race for first exciting, but also the race to avoid relegation entertaining. In American sports, last place teams often simply give up, a disappointment for fans. 

I wanted to see exactly how promoted/relegated teams fared throughout the season. Some statistical research has already been done on the subject: Omar Chaudhuri, writer of the 5 Added Minutes blog, looks at conversion rates of promoted teams and their corresponding ability to stay in the top flight here.  In part 1 of this post, I have looked at how promoted teams have done in their first season in the top flight. My original idea was that teams may struggle early in the season to adjust to the higher level of competition, and eventually even out as the weeks go on and the teams adjust. This also puts the performance of QPR, Swansea, and Norwich into perspective with past promoted team's performances. I use data from promoted teams from the 2003/2004 to 2010/2011 season. 

I've created 5 graphs to illustrate the performances of promoted teams. The first one, below, shows how all the promoted clubs' point totals have progressed over the 38 games. On average, promoted teams earn around a point per week. The greenish linear-looking line in the middle is the average. All the other jagged lines are the point totals over the season of promoted clubs. This graph isn't too informative, but is an interesting graphic nonetheless.

The next graph is the same as the one above, but only looks at the three promoted clubs this season in comparison to the average points line and the linear points line. To clarify,  the linear line shows is a line illustrating what would happen if a team earned the same points every week to end up with the average point total for promoted clubs. The average line shows the average points earned each week of the season. These may sound the same at first, but I will show in the next couple of paragraphs that there is an important distinction. Anyways, the graphic below illustrates that all 3 promoted clubs are faring about as well as the average promoted team does. QPR started off a little stronger, but has since returned to the average. Norwich and Swansea both started a little weaker, but have improved to end up just above the average 7 weeks in to the season. All 3 teams have 8 points so far, just above the point per week average of promoted teams.

Another way of looking at the first graph is by looking at points per game of promoted teams. The graph below shows this. Obviously, at first clubs' point per game total is a little spread out. As the season progresses, teams earn an average of 1 point per game, as mentioned above. Some clubs have done a little better, and some a little worse, as evident from the graph.

Next is the graph above, but again looking at the performance of the 3 promoted teams this season. Again, the graph shows that QPR started off the campaign a little stronger, but has since regressed to be even with Norwich and Swansea.

The final and most informative graph shows the cumulative points per game of promoted clubs. This graph answers my question of how promoted teams fare throughout the season. As you can see below, promoted teams seem to struggle up until week 7, where they turn it around and do better than their average point total up until around week 20, where they hover around the point per game mark until the end of the season. There could be a lot of explanations for this trend. Maybe clubs struggle at first, and then adjust to the higher competition? Maybe clubs transfer window acquisitions (think QPR) start to pay off around week 7? It would be tough to tell what the true factors driving the trend are really. However, the graph does highlight the interesting phenomenon. 

I'm still working on doing a similar analysis of clubs that are relegated at the end of the season to analyze how their performance fluctuates throughout the season.

Expected Points Added (EPA) Leaders Through Week 3

Below are the Expected Points Added (EPA) leaders for the EPL through week 3. The week 1 leaders can be found in an earlier post here. To reiterate, EPA weights goals based on how important they are to the team's chance of winning the game. This is based on the notion that a go ahead goal in the 90th minute is worth more than the 5th goal in a 5-0 win.

Some interesting things to point out...

• While Rooney has 5 goals this season, Welbeck's 2 goals have actually been more beneficial to United. In fact, Rooney doesn't even make the top 15 list above considering most of his goals were in the recent Arsenal blowout.

• Dzeko gets to the top of the list by scoring frequently and in important situations. His average goal weight is a solid .51 expected points added, but just because of the fact that he has scored 6 goals puts him at the top.

• It's still early in the season. Arteta makes third on the list with only 1 goal (a late game winning goal). Soon we'll start to see the top dominated by players who have scored a lot, and in important situations.

Expected Points Added (EPA) Data Through EPL Week 1

Before the season I promised to post Expected Points Added (EPA) totals after each week of the season. Here are the EPA totals from week 1. If you don't know what EPA is, check out a full explanation here.

To summarize it very basically, EPA is the total measure of how much each player's goals add to team's expected points total. That is why you see some EPA's of 0 below. These players scored goals that added nothing to the teams expected points total (for example, a team is up 3-0 and is already going to win, and a player scores a 4th in the 90th minute. This does not add to the team's chance of winning technically, because the team is already very likely to win.)

Average Goal Weight (AGW) is just EPA divided by the number of goals a player has scored. This measures how important, on average, a player's goals are. It can show us that a player consistently scores clutch goals (high AGW) or that they are scoring useless goals in blowouts (low AGW).

Dzeko has the highest EPA from his go ahead goal in the 57th minute. This equated to a little more than a point for City. Klasnic, Muamba, and Silva all scored goals that added no expected points for their team.

If you have any questions feel free to ask in the comment section. I'll be super busy this week between moving in to my apartment at school and 3-a-days for preseason but I'll try to keep some posts coming.

Why We Shouldn't Put Much Value in Assists

Last week I wrote a post on why shots on goal are a misleading statistic. In keeping with the analysis of the problems with some commonly kept statistics in football, I decided to look at assists. 

If you think about it, assists are highly misleading. Simply playing with good players boosts your assist total. Similar to shots on goal, not all assists are the same. There are the assists where a player makes a short pass in the midfield that leads to a teammate dribbling through all the opposing defenders and finishing, and the assists where a player makes a beautiful cross where their teammate simply has to tap the ball in the open net. These obviously shouldn't be counted as the same value to the team, yet they are. Hell, I could probably record an assist eventually in the EPL if I played for one of the top teams (OK, maybe an exaggeration but you get the point.)

First, let's look at the assists data for all the teams in the EPL league. As the graph below shows, as the point value of a team increases (basically, the better the team is) the assist total also generally increases. This is no surprise. We would expect better teams to score more goals and thus have more assist totals.

Basically what this means is that the assist statistic should favor players on better teams. Players on better teams play with better teammates and should therefore have more opportunities for assists. Below is a screenshot from the EPL website of the players with the top 20 assist totals.

9 players from top 5 clubs are in the top 20 for assist totals. No players from bottom 3 clubs are in the top 20, with the exception of Blackpool's Charlie Adam who was just signed by Liverpool. It's easy to see assists totals are higher for players on better clubs.

A better statistic that is not influenced by the quality of your teammates are chances created. A chance created is defined as a pass that leads to a shot. These are obviously not as dependent on your teammates and give a more fair and true assessment of how much of a playmaker that player is for their team. 

The next time a club is looking to sign a player based solely on their assists totals, they should take a more in depth look. Assists can tell an inaccurate, or at the least biased, story.

An Analysis of City Pre/Post Abu Dhabi Using the Transfer Price Index

Pretty soon I'm going to start writing the Manchester City statistical blog over at http://www.eplindex.com/ (@EPLIndex). I also just read Pay As You Play by Paul Tomkins. If you haven't read it and you're interested in statistics and football, you should really give it a read. The book basically outlines the trend in the EPL that money buys points using what Tomkins calls the Transfer Price Index. More specifically, the higher the cost of the XI (Tomkins refers to this as £XI) the more a team tends to win. Of course, there are exceptions to this, but in general it seems to hold true. Anyways, when I was reading the book I thought it would be a good idea to analyze City using Tomkin's data, especially when I saw that my future fellow City blogger at EPL Index Danny Pugsley (@danny_pugsley) wrote the "Expert View" for the City section. I'm no expert on the analysis that Tomkins does, but I understand a good amount from reading the book. The subject of the book rings especially true for City considering the recent Abu Dhabi takeover and sudden influx of large amounts of cash for the club.

Some notes before the analysis: One, the data I am using is all from the book Pay As You Play, as I mentioned above. Two, make sure to notice some data is missing for years when City was not in the top flight. Three, the data in the book only goes to the 2009/2010 season, so the 2010/2011 season is missing.

Basically, I looked at 3 questions: 1.) Does City really spend more money since the Abu Dhabi take over? 2.) Does a higher £XI cost equate to success for City in the EPL? 3.) Screw 1 and 2. What if City keeps buying Robinho's?

Does City really spend more money since the Abu Dhabi take over?

Yeah, really dumb question. Pretty obvious the answer is yes. Below is the graph comparing the league average starting eleven cost and the City starting eleven cost since 1992. In the 2008/2009 City's £XI is higher than the league average for the first time since the 1994/1995 season. Remember, Abu Dhabi took over at the start of the 2008/2009 season. For the 2009/2010 season it skyrockets to over £120,000,000. City now has money to spend.

Does a higher £XI equate to success for City in the EPL?

The answer Tomkins gives for EPL clubs in his book is yes. Again, this makes sense. Clubs that are able to spend more on players should be able to produce higher quality sides and win more. I wanted to analyze specifically City's success, so I looked at the data to see if their £XI rank in the EPL follows their league position. In other words, does City succeed more when they spend more? Looking at the graph below, the answer seems to be yes. The league postion (green line) generally follows the club's £XI rank (orange line).

Screw 1 and 2. What if City keeps buying Robinho's?

The first two graphs seem to point to inevitable success for City. They have a lot of money and money can buy success, so they'll succeed, right? People will obviously point to some recent not-so-successful expensive purchases. Robinho, Jo, and Santa Cruz are the 3 big ones. Each has had start percentages of 47, 16, and 16 respectively, despite a massive total cost of £69,000,000. A good graphic to show the efficiency of purchases is the cost per point used in

Pay As You Play

. Clubs that are efficient in this regard will have spent less money per point earned, while clubs that are inefficient will do the opposite. The graph shows how much City spent in each year for each point they earned. Not surprisingly, the cost per point has spiked since 2008. This may seem like money is being wasted. While City may not be getting as much bang for their buck, it likely won't matter in terms of success. According to Tomkins, the highest cost per point goes to Chelsea in 2006/2007. They finished in 2nd that year. It seems that simply having a lot of money can trump inefficiencies displayed from the cost per point value. Tomkins even refers to City's high cost per point on page 18: "Manchester City will certainly close the gap for this unwanted honour (although if they win the league, they won't care what people think; they could probably afford to pay £4m or £5m per point if it would guarantee them success)." So yes, City may make some poor purchases like Robinho, Jo, and Santa Cruz in the future. All in all, it doesn't matter that much though. City has so much money that they'll win anyways.

Another Look at Referee Bias: Extra Time Given

Yesterday I looked at referee bias in this past season for the EPL. It turned out that while referees favored the home team overall in parts of the game like fouls, yellow cards, and red cards, it is more likely due to the advantage the home team has in a game. One statistic I did not look at though, is the amount of extra time given.

Extra time has nothing to do the relative abilities or score of the game like many other parts of soccer do. In theory, it should be an objective amount not dependent on if the home or away team is leading in the game. You see in almost every game though, the home crowd jeering for the ref to end the game if their team is ahead, or cheering even louder for their team to come back if they are trailing. Based on this, referee bias would be present if home teams that are leading have shorter games compared with away teams that are leading. The obvious logic being that the referee gives in to the home team's fans and adjusts his extra time given unconsciously.

To do this I looked at the length of the game for home teams that won the game versus length of the game for away teams leading. If there is indeed a referee bias then we should see that the length of games is shorter for home leading teams versus away teams.

Below are histograms (graphs showing the frequency of each dependent variable value) of the length of the game for the two categories above.

We can see the graphs are very similar, except for the tail on the right end of the away win time. This is in accordance with our hypothesis that away teams that are leading face more extra time. It seems refs gave trailing home teams more than 10 minutes of stoppage time more than they gave trailing away teams more than 10 minutes.

Like the previous post looking at referee bias, I did statistical analysis to see if the difference was actually statistically significant (in other words, the difference was not due to randomness). The mean length of game for leading home teams was 96.36 minutes, while the mean length of games for leading away teams was 96.56.

Using the data, I ran a two sample t-test. Basically what a

 t-test does is takes in to account the number of observations, mean, and standard deviation (measure of spread) and tests to see if they are equal. In the end, the test gives a p-value between 0 and 1. A p-value basically answers the question, if the two means were actually the same (time given for leading teams were the same for home and away), what is the probability that we there would be a difference in the means that we actually saw. In this case, a probability of 0 suggest that the means are different, and one of 1 suggests they are the same. Generally, a p-value of .05 or lower is statistically significant, meaning we can rightfully say the means are not the same.

After doing the test, the p-value I got was 0.2013. While this suggests that referees are giving more time to trailing home teams, it is not at a statistically significant level. In other words,

we cannot conclude that referees give more extra time to trailing home teams compared with trailing away teams.

 It may seem like there is a bias evident based on the means, but it is not at a statistically significant level.

All in all, referees are doing a good job in terms of not favoring home teams over away teams. Next time someone complains that the ref is favoring the home team, you can just tell them to look at the data.

WPA and AGW: Van Persie is overrated

Well, maybe the title is a little exaggerated. What I really mean is the value of Van Persie's goals last season are overweighted. On the other hand, Darren Bent's goals were undervalued. The explanation comes from WPA, or "win probability added".

If you read the last post, I explained win probability. If not, check it out here. Because we have a probability for every game situation, I was able to weight goals by the added win probability a team has from that goal. In soccer, is a little more complicated because teams can tie. To solve this, I use win percentages instead of win probability. To get a team's win percentage you weight a win as 1 point, a draw as 1/3 of a point, and a loss as 0. The sum of these divided by the number of games a team has played gives us the win percentage. I guess in this case it should be win percentage added instead.

The added part comes in by calculating how much a goal adds to a teams win percentage. Here are a couple of examples:

-A goal in the 95th minute to put the home team up by a goal would have a WPA of .666666. A tie game in the 95th minute gives the home team a win percentage of .33333 (almost every time they will draw the game). However, in this case the home team scored. Now the score is 1-0 in the 95th minute. Now the home team's win percentage is almost 1 (almost every time they will win the game). To get the WPA of the goal we subtract the win percentage before the goal (.3333) from the win percentage after the goal (1). This gives us a WPA of .666666

Basically what WPA does is values goals that are more important to the team. In the example above, that goal is obviously very important to the team. However, a goal in the 90th minute to put a team up by 6 would be worthless to the team. That goal would have a WPA of 0.

I calculated the WPA of the top scorers in the EPL last season (players with more than 10 goals). Interestingly enough, the list shook up a bit. The table is below.

Notably, Darren Bent moves up to first on the list, and Van Persie moves down to 8th. Beyond this, I wanted to know which players tend to score more important goals and which players score non-important goals. Obviously, Van Persie has a higher WPA than most of these players because he scored a lot more goals than them. 

The way I did this was to calculate the average WPA of a goal by a player. I called this the Average Goal Weight, or AGW. The list of the AGW versus goals is below.

Not surprisingly, Van Persie moves to the bottom of the list, and Bent stays at the top. So what does all this mean? I don't think its a good idea to jump to the conclusion that Van Persie is not a good goal scorer. Despite everything, he scored 18 goals last season, which is good no matter how you score them.  However, I think AGW is a good supplement to the top goal scorers list. Last season, Bent was consistently scoring goals that added a whole 10 points to the winning percentage than Van Persie on average.

You shouldn't base your entire assessment of a goal scorer only on AGW. However, I think its something to take in to account.

Win Probability Added in Soccer

Everyone hears it all the time: A 2-0 lead is the most dangerous lead in soccer. But is it really? Thinking about the led me to wonder how exactly dangerous leads were in soccer. In fact, I wanted to find out what win, loss and draw percentages a team had in all situations. The best way to find this out is to analyze a lot of games and calculate the win, loss, and draw percentages in every possible game situation. To do this, I took in to account the venue of the game (home versus away), the goal differential between the teams (team is up by 2, team is up by 1, game is tied, team is down 1, team is down by 2 etc) and the minute of the game. I took goal differentials of -5 to 5 and minutes 1-90. I thought these were probably really the most important factors. You could maybe take in to account cards too, but this is hard and makes it pretty complicated. Overall, there are 2*11*90 = 1980 combinations of game situations.

The idea relates to WPA in baseball. Basically, WPA is a measurement of how much a play adds to the chance the team wins a game. For example, how much does a 2 run home run help the team's chances in the 6th inning? In soccer, a question would be how much does a goal at home to give you a 2 goal lead in the 67th minute change your winning percentage in the game? Pretty simple concept.

To get the percentages for all of these situations I imported game data from the past 10 years of the EPL in to Excel. My Excel skills are not the best but with some help I was able to eventually get these to convert in to percentages for each game situation mentioned above. The basic idea is this: how often do teams with a 1 goal lead in the 40th minute at home win? How often do they draw? How often do they lose? This was done for every minute and every goal differential both home and away. The results truly tell us how dangerous a variety of leads are.

Here's an example: The team is away, the game is tied, and it's the 67th minute. Any guesses on the win, draw and loss percentages? Well turns out the team has about a 19% chance of winning, a 51% chance of drawing, and a 30% chance of losing.

We can also test the "2 goal leads are the most dangerous leads theory". Let's say the team is home and it's the 35th minute. Here are the percentages for 1 and 2 goal leads:

1 goal lead: win: 78%, draw: 16%, loss: 6%
2 goal lead: win: 96%, draw: 2%, loss: 2%

The same holds true for all minutes and both home and away teams. A 2 goal lead is in fact not the most dangerous lead in soccer.

I'm also in the process of making a Java Applet to post here that lets you input the goal differential, venue, and minute, and spits out the win, loss and draw percentages. Again, my Java programming talents are not the best, so no promises on anything getting finished or uploaded soon. I uploaded the actual excel files to a google sites page though if you're curious to look at other percentages. If you want to download the files click here and type in the search bar ".htm" without the quotes to find the files.

Next, I'm planning on relating this more to how WPA is used in baseball by using it to analyze specific players by calculating how much percentage they add to their team winning by scoring goals. Not sure how useful this statistic will actually be, but it's worth a shot.